Informacje o artykule
DOI: https://www.doi.org/10.15219/em80.1421
W wersji drukowanej czasopisma artykuł znajduje się na s. 34-44.
 Pobierz artykuł w wersji PDF
Pobierz artykuł w wersji PDF
 Abstract in English
Abstract in English
Jak cytować
Kopczewski, T. & Okhrimenko, I. (2019). Playing with Benford's Law. e-mentor, 3(80), 34-44. DOI: 10.15219/em80.1421
E-mentor nr 3 (80) / 2019
Spis treści artykułu
- Abstract
- Introduction
- History, formulation, and testing of BL
- Application of BL in teaching economics
- Experiment, simulation, and research - BL in the classroom - a case study
- Conclusions
- References
Informacje o autorach
Przypisy
1 Labsee.com is a platform designed for conducting large-scale online economic experiments.
2 One can find the R-project to generate the presented visualizations in the online annex; alternatively, there are ready-to-use visualizations (see Fig. 4).
Playing with Benford's Law
Tomasz Kopczewski, Iana Okhrimenko
Abstract
This paper presents a classroom experiment, the simulations, and a research which familiarize the students with the Benford’s Law. This law is widely used in a tax fraud detecting procedures. This paper shows that: i) the Benford’s Law can be useful in extending the simple perception of the probability which is presented at the lectures concerning the risk, ii) can be an excellent example of using data processing for the classroom tasks, iii) by the experience of the fraud detecting technique the students might change their attitude to cheating. The experiment and the prepared R codes can be used in the numerous courses, such as accounting, applied microeconomics, and quantitative methods.
Keywords: Benford’s Law, probability perception, tax fraud, scientific fraud, R-CRAN
Introduction
Benford's Law (BL) can be defined as a collection of empirical evidence related to the frequency distribution of the leading digits in numerical data sets. The best-known version of the law states that in those data sets representing a collection of "natural" data, the probability of seeing a particular digit in the first position is inversely related to its rank. For example, 1 appears as the first digit in about 30% of all cases, while 9 appears in less than 5% of cases. Other versions of BL define the frequency distribution of the second digits, third digits, and their combinations. The history of the discovery of this law makes it even more mysterious. Initially explored by Newcomb (Newcomb & Nuw, 1881), the law was forgotten for more than 50 years. Benford (1938) rediscovered it, and used it to explain the behavior of numerous data sets from different domains of science. BL can be treated as one of the most exciting representations of the power laws, which are used in natural sciences and empirical research in economics (Gabaix, 2016).
In real-life numbers are assumed to be defined by random events, thus following BL. However, our perception of randomness deviates from true randomness. Falk & Konold (1997) note that the human mind tends to produce rather dense distributions, assuming that the probability of any digit taking first position is equal for all digits. In other words, we expect digits to be uniformly distributed, and the chances of seeing any digit in the first position are equal (with a chance of 1/9 ≈ ∽ 11.1%). If the numbers are generated by the human mind, the distribution of the first digits should differ from Benford's distribution. Therefore, BL can be used as a test for whether a dataset contains real-life numbers (Gauvrit et al., 2017). A particular area of BL application is in the fight against tax fraud (Drake & Nigrini, 2000).
The popularity of BL, especially in the accounting textbooks, rises as big data analysis enters everyday accounting practice (Janvrin & Watson, 2017). However, the application of BL should not be limited solely to these areas; it seems that not only accounting and finance, but other fields of economics can be enriched by introducing BL to the academic curriculum. The present paper utilizes a simple tax fraud classroom experiment based on BL in order to achieve the following teaching goals: i) demonstrating to undergraduate economics students the complexity of probability theory as well as biases related to "folk" probability estimation in the human mind; ii) showing the opportunities for big data analysis; iii) discussing the reliability of publicly available data and ways to check it; iv) familiarizing the students with simple programming tools for simple applied economic problems.
The first part of the paper discusses the history of BL, its functional form, and its application in anti-tax fraud procedures. The second part is devoted to the potential of BL to enrich the academic curriculum of different economics subjects. Finally, the third part presents the detailed guide for the lecture devoted to BL, including classroom experiment methodologies and relevant empirical and theoretical support.
History, formulation, and testing of BL
The history of BL began in 19th century when an astronomer, Newcomb (1881), noticed that the first pages of the logarithm books in the library were the most thumbed, while the last pages left relatively undamaged. He explained this by the fact the frequency of distribution of the first digits is not uniform and is instead inversely dependent on the digit's rank. Initially, this distribution pattern was defined as

where
D is the digit's rank;
PD is the probability of seeing digit D as the first digit in the randomly chosen number.
Equation (1) implies that probability PD of the first digit D occurring, which takes the value from the range D∈[1,9], can be defined as a common logarithm of  . If the distribution of the first digit was uniform, the probability of any specific digit occurring as the first digit would be identical for each digit (approximately 11.1%). However, according to the Newcomb's formula for probability distribution (1), for the digits 1, 2, and 9, the probability of appearing as the first digit is close to 30%, 17%, and 4%, respectively. The pattern is general and irrespective of the unit of measurement or data source, and thus is referred to as a "universal property of real world measurements" (Sambridge & Tkalčic, 2010), or, more poetically, the "harmonic" nature of the world (Furlan, 1948). The law was rediscovered by Benford in 1938, who analyzed 20,229 numbers related to city populations, financial data, etc. from 20 different statistical sources, and proved that the distribution of the first digits followed the pattern he defined.
. If the distribution of the first digit was uniform, the probability of any specific digit occurring as the first digit would be identical for each digit (approximately 11.1%). However, according to the Newcomb's formula for probability distribution (1), for the digits 1, 2, and 9, the probability of appearing as the first digit is close to 30%, 17%, and 4%, respectively. The pattern is general and irrespective of the unit of measurement or data source, and thus is referred to as a "universal property of real world measurements" (Sambridge & Tkalčic, 2010), or, more poetically, the "harmonic" nature of the world (Furlan, 1948). The law was rediscovered by Benford in 1938, who analyzed 20,229 numbers related to city populations, financial data, etc. from 20 different statistical sources, and proved that the distribution of the first digits followed the pattern he defined.
BL can be extended to other systems besides the decimal. The more general form of BL is presented in equation (2).

where
D is the digit's rank;
B is the number of digits in the system (for instance, for a binary system, B=2).
It is possible to define the distribution pattern not just for a single digit D, but also for a combination of n digits. Table 1 presents the precise expected frequency of the first four digits in accordance with Benford's distribution. Figure 1 shows the probability distribution function for the first digit, which is the most commonly applied.
| Digit | Probability of occurring in the first position | Probability of occurring in the second position | Probability of occurring in the third position | Probability of occurring in the fourth position |
| 0 | N/A* | 0.11968 | 0.10178 | 0.10018 |
| 1 | 0.30103 | 0.11389 | 0.10138 | 0.10014 |
| 2 | 0.17609 | 0.10882 | 0.10097 | 0.10010 |
| 3 | 0.12494 | 0.10433 | 0.10057 | 0.10006 |
| 4 | 0.09691 | 0.10031 | 0.10018 | 0.10002 |
| 5 | 0.07918 | 0.09668 | 0.09979 | 0.09998 |
| 6 | 0.06695 | 0.09337 | 0.09940 | 0.09994 |
| 7 | 0.05799 | 0.09035 | 0.09902 | 0.09990 |
| 8 | 0.05115 | 0.08757 | 0.09864 | 0.09986 |
| 9 | 0.04576 | 0.08500 | 0.09827 | 0.09982 |
Source: Nigrini, 1999, p. 2.
* The probability cannot be defined.
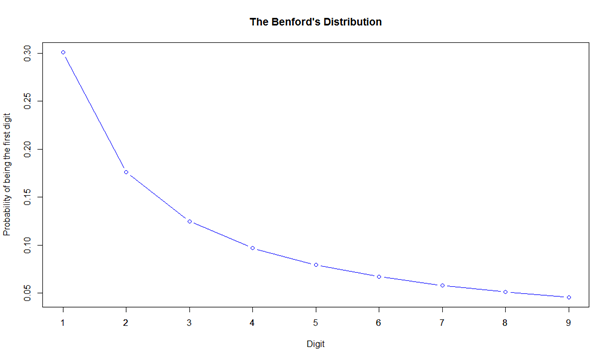

Source: authors' own work, based on Nigrini, 1999, p. 2.
The explicit and unified theoretical justification of BL still has to be developed (Sambridge et al., 2011; Berger & Hill, 2011). Nevertheless, the attempts to design it have resulted in the theorem of random samples from random distributions. This theorem suggests that even if some individual distributions of real data do not follow BL, random samples taken from such distributions still do (Hill, 1995). As discussed in the next section, numerous studies have explored the opportunity to exploit BL for the sake of uncovering tax fraud. From this perspective, the researchers need statistical tools that can provide reliable results concerning the deviations of the hypothetically "natural" data samples from the distributions predicted by BL.
One of the most common methods of testing the consistency of theoretical and empirical distributions is the goodness-of-fit test. The null hypothesis (H0) states that a sample of the data does not differ from the sample predicted by BL. The test statistics have the typical Chi-squared distribution (Cho & Gaines, 2007, p. 220):
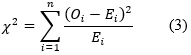
where Oi is the observable frequency of digit i;
Ei is the expected frequency of digit i (i.e., frequency predicted by BL);
n is the number of observations.
This follows from Chi-squared distributions with k degrees of freedom. One of the major disadvantages of this test is that it is extremely sensitive to sample size, which makes it too rigid for testing purposes (Ley, 1996; Giles, 2007).
One possible alternative might be the Kolmogorov-Smirnov test for comparing two empirical distributions by defining the largest absolute difference between the cumulative distribution functions as the measure of the discrepancy:

where k is the total number of observations;
Fn1 (x) and Fn2 (x) are empirical cumulative distributions of the first and the second sample, respectively;
n1 and n2 are the sizes of the first and the second sample, respectively.
According to Stephens (1970), the Kolmogorov-Smirnov test is not biased by sample size and gives more reliable conclusions. However, as noted by Noether (1963), tests based on the null hypothesis of a continuous distribution may not be appropriate for testing discrete distributions. As a result, the test values may be quite conservative in rejecting the null hypothesis, giving false-negative results.
Application of BL in teaching economics
Accounting and finance - tax fraud
The first proposal for applying BL to check the validity of natural number samples was made by Varian (1972). However, BL was still not applied by accountants and tax officers up to the late 1980s, when Carslaw (1988) observed that the distribution of the digits in data reflecting income streams from New Zealand was not in line with BL. Nigrini's works (1996; 1999) on the digital analysis were actually helpful in uncovering cases of tax evasion in the USA. At the same time, some researchers (see Ettredge & Srivastava, 1999) stated that the fact that the distribution of the first digits in the presumably real numbers differs from BL does not necessarily imply fraud: the deviation might arise from flaws and operating inefficiencies in the operating data systems.
Durtschi et al. (2004) defined the cases when BL should or should not be applied in order to recognize fraud. They claim that BL can be used as a reliable detector of fraud i) when the numbers are the combinations (products) of the other numbers (e.g. sales); ii) when the dataset is large enough; iii) when the mean is higher than the median, and the skewness is positive. In contrast, BL will not give reliable conclusions about fraud when: i) the numbers are assigned (e.g. invoice numbers); ii) the numbers are the product of human design (e.g. prices, which tend to end with 99); iii) the numbers come from accounts featuring a large proportion of firm-specific numbers, and iv) when there are minimum and maximum numbers built in.
The last couple of decades have been marked by a substantial increase in the volume of financial and accounting literature showing how to use BL to track fraud and its applicability in forensic accounting (Nigrini, 2012). The know-how presented in the majority of papers focused on the operational side of the problem (Simkin, 2010). The focus on the applied aspects of BL in the accounting and financial literature caused the development and extension of these methods (Nigrini, 2012). New and promising areas of application in finance and accounting are anti-money-laundering (Yang & Wei, 2010) and financial statement analysis (Henselmann et al., 2012). Drake's and Nigrini's (2000) methodology can serve as an excellent example of how to introduce BL and digital analysis of accounting data to students efficiently. This paper can be treated as a very comprehensive instruction for students and practitioners of accounting and auditing.
Microeconomics - training the probability perception
The critical issue related to the modern way of teaching microeconomics is the excessive use of the "chalk-and-talk" approach as well as insufficient attention towards the students' skills of solving applied problems (Watt, 2011). A BL experiment can be treated as one of a series of activating tools used during applied microeconomics courses. Its main aim is to show how the simplified perception of the probability can result in incorrect perceptions of real-life economic phenomena. Even setting up a simple standard model requires, among other things, a realistic understanding of the probabilities, which is usually outside the agenda of an economics education (Gigerenzer, 2015). The majority of economics textbooks present problems where the probabilities are either explicitly defined or can be derived using simple rules of probability counting (see, for instance, McConnel et al. 2014, Varian 2014, Frank & Cartwright 2013). Students do not gain any skills in evaluating probabilities on their own; instead, they obtain the information as found in textbook problems.
BL can be treated as one of the Power Laws (PLs), which are a good source of the empirical evidence necessary to develop the skills of realistic probability perception since they facilitate the process of gaining background knowledge about the numerous empirically observed patterns. Firstly, PLs are present in various fields of science and life. One of the best known and commonly mentioned beyond the field of formal science is the Pareto principle, while an additional example is that the size distribution of cities follows Zipf's Law (1936), analogously to the size of the companies and the stock exchange cumulative returns (Gabaix, 2016). Secondly, the unique thing about PLs is that they break the common perception that the variables are distributed around the mean (i.e., that data generally fit the uniform or normal distribution patterns). Our tendency to average is so strong that even the popular Pareto distribution of income is flattered in the human mind, as Norton and Ariely (2011) showed in their experimental study.
Big data - the new challenge
The development of the field of data science has provided additional opportunities for applying statistical analyses, such as testing BL in many areas of management, accounting, business, and economics. It is part of the "big data" revolution, in which various data are treated as a new production factor. Big data is referred as "high-volume, high-velocity and/or high-variety information assets." (Gartner, 2015, retrieved from Janvrin & Watson, 2017, p. 2). The field of data science as it is understood nowadays is relatively young, but it has already become integral to a wide range of related fields. Teachers need to find a new way of incorporating this change to the existing educational process.
Janvrin and Watson (2017) have analyzed the role of big data in maintaining accounting standards. The big data approach is even more relevant to revealing cases of tax fraud by applying BL because using automated procedures is less costly than developing the human mind. Further developments in data science and the standardization of reporting methods for the tax and financial authorities may also facilitate the development of automated audits. For accounting students, the new tools provide the possibility to analyze both structured and unstructured data using Business Intelligence (BI) technologies and avoiding time-consuming and laborious calculations in Excel. BL is set to become part of the curriculum for accounting students (Drake & Nigrini, 2000).
The big data revolution will also change how we teach economics. The new IT tools make statistical analysis simpler and easier. Admittedly, economics students have no access to typical BL tools due to the relatively high costs, but the combination of open-source R, R-studio and Markdown software makes it possible to conduct studies with no explicit costs. The availability of ready-to-use procedures allows them to carry out such data exploration with little in the way of programming skills and can be a good motivator to learn how to code and to use statistics. The possibility of testing BL seems to be wide open for students and teachers. The increasing number of emerging areas and applications make it more attractive (Berger & Hill, 2015). There are two main areas of using BL in the classroom: i) testing the quality of economic data, and investigations related to scientific fraud and fake data; ii) testing the behavior of forecasts in econometric modeling.
Similarly to tax and financial data, economic data may contain defects resulting from unreliable reporting or intentional manipulation. The exploitation of the data should be preceded by procedures for testing data quality. The literature showed that the credibility of the data used in economic and social science research is moderate or even low (Ioannidis & Doucouliagos, 2013). BL is one of the potential tools available to investigate the problem of data falsification (Michalski & Stoltz, 2013). The application of these new IT tools makes the procedure so simple that even students can become investigators and discover scientific fraud and non-naturality in the data. This can be their first step towards critical thinking about scientific evidence. The experience of investigations of this type can also reduce the moral hazards of students by demonstrating the existence of efficient tools for detecting fraudulent behavior.
An additional and relatively new area of using BL is an application for testing the robustness of the forecasts in econometric modeling. If the input data fits BL, then the output data should also meet the same criterion. The new evidence shows that some outputs from numerical algorithms, transformations of the random variables and the stochastic processes, as well as multidimensional systems, fulfill BL (Berger & Hill, 2015). A test based on BL may be an exciting proposition to evaluate such models as Dynamic Stochastic General Equilibrium Models (hereafter DSGE), which have no statistical goodness-of-fit measures yet.
Experiment, simulation, and research - BL in the classroom - a case study
The educational tools presented in this section were used to introduce BL during an Applied Microeconomics course, but they can also be used for accounting/finance or data science classes. The first stage of the study is to conduct an experiment; the students have no prior knowledge when providing the answers, and this is expected to have a positive effect on their motivation to learn the subject through the creation of a form of "information deprivation". The second stage is devoted to the analysis of BL, including the theoretical formulation of legal, real-life examples, and an application of BL in tax fraud detection. The demonstration of the Monte-Carlo simulation is presented to prove the evidence collected by other authors. Finally, the students' answers are presented. The third stage of the study incorporates an analysis of the IT tools necessary for conducting the experiment and the data analysis.
The tax fraud problem was the central storytelling (or narrative) framework, used to make the problem interesting for the students. To be more precise, they attempted to fool a hypothetical tax officer through providing fictional numbers that appeared to be random. Geyer (2010) used a similar methodology, making BA students play the role of tax evaders. The crucial difference between Geyer (2010) and the present paper is that the latter proves explicitly to the students the impossibility of committing tax fraud in the epoch of big data techniques. In other words, the undergraduate economics students gain valuable experience, which is expected to prevent them from cheating in the future.
The main goal of using the tools was behind the story. It was attempted to show to the students that: i) the straightforward perception of probability can result in inefficiency in the analysis of real-life problems; ii) the possibility of fraud in the big data era is much smaller, and this is explained not only by the tax and financial issues but also by developments in scientific research and public statistics.
Conducting the experiment
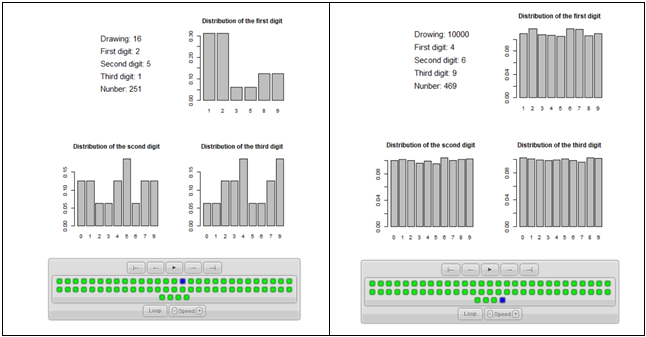
During the experiment, the students were asked to add 60 numbers to the fictitious invoices. Their goal was to generate data that would appear to be generated by random factors, not by the human mind. The students received a small number of additional grading points for participation in the experiment, and they also gained extra points for avoiding being caught. The incentive may seem to be non-ethical, as the students received extra points for non-ethical behavior; however, the motivation incentive scheme is correct. The chance that they would receive points for efficient cheating is minimal, as the anti-fraud procedures based on BL work fine. Even after the lecture, a student who knew and understood BL had problems with fictional cheating on the tax authorities because they could not control the frequencies of all the digits. In addition, the students need to experience that their effort to cheat is useless. This experience (i.e. demonstrating how easily fraud can be detected) is a crucial factor, which can influence their further behavior and motivate them to avoid fraud (Joyner, 2011), especially in the light of the public presentation of the results of anti-fraud procedures. In order to avoid the possibility of boycotting the experiments caused by the transparency of the decision, the students were asked to enter an anonymous nickname during the experiment (see the first screen of the experiment, Fig. 2). They could recognize their results while remaining anonymous on the animation presenting the results of the antifraud algorithm (see Fig. 2).


Source: authors' own experiment, programmed in labsee.com.
The experiment is quite short and can be conducted as the first part of the lecture or as prior homework. The students have to fill in the gaps with numbers on all four screens representing the hypothetical monthly accounts (see Fig.3). To make the task more complicated, the students must enter the numbers using a pre-defined number of digits.
The experiment was conducted using the labsee.com platform1. The platform offers a variety of tools for conducting online synchronous and asynchronous experiments and surveys; using this platform requires basic skills in Java programming. The advantage of the using labsee.com platform is the instructor's ability to control the experiments in real-time during the lecture. However, if the experiment is performed asynchronously, the instructors are free to use any other online platform.
Introducing BL by the simulation and analysis of real data
After all the participants submit their responses, the instructor should proceed to introduce and explain BL. The proposed method of doing this is split into several stages: i) explaining BL using the Monte Carlo simulation and theory presented in the first section of the present paper; ii) proving that real-life data follow BL; and iii) showing and discussing the results of the experiment.
The Monte Carlo simulation serves as a simple thought experiment, which shows the misleading perception of a probability based on the prior student's experience about the distribution of values around the mean. In the first part of the experiment, they should imagine one bag containing nine ping-pong balls, labeled from 1 to 9, and the other two bags containing ten ping-pong balls labeled from 0 to 9. If the participant is asked to close his eyes and withdraw a random ball from the first bag, what would be the probability of pulling out a ball labeled "7"? According to theory and common sense, the probability should be 1/9. The same would be applicable to any other number. For the second and third bag, the probability of pulling out a ball with a random number should be 1/10. The MC simulation ball_drawings.html2 presents the visualization of the sequential drawings, which mimics the process of the random choice of 60 samples from three digit numbers (see Fig.4).

Source: authors' own analysis in R in animation package (Xie, 2013).
The main observation that should be stressed based on the simulation is that for a small number of repetitions, it is difficult to find any patterns in the generated data. However, as the number of draws grows, the probability is consistent with the expected uniform distribution (the last screen shows the results of 10000 draws). After this simulation, it is the right time to introduce BL using the suspense technique. The teacher should ask the students whether they used the kind of reasoning presented in the Monte Carlo simulation. The majority of students will probably confirm this. Then the teacher should follow the narrative structure and create the tension by announcing that if this was their strategy, then they have been caught on cheating on the invoice experiment because the actual distribution of digits is significantly different.
The instructor should present visualizations of the first digit distribution in the empirical datasets in order to show that natural data flows suit BL. The visualization empirical_data.html includes four data samples. The first three are real data describing: i) the lengths of the 98 longest rivers in the world; ii) the populations of the majority of countries; and iii) the GDP of the majority of countries, respectively. The fourth data set is the Input-Output (I-O) matrix used in the estimation of the DGSE model (Kiuila, 2018). The visualization (see Fig. 5) shows that even for a relatively small number of observations, it is easy to see a common pattern in the distribution of first digits (Fig. 5a). The first digits are not uniformly distributed. For any digit, the frequency of occurrence in the first position is inversely related to its rank: for instance, the digit 1 is much more frequent than the other digits. For the full sets of observations (Fig. 5b), the distribution of all the data is nearly identical and follows BL.


Source: authors' own analysis in R in animation package (Xie, 2013).
Discussing the results and post-experimental activities
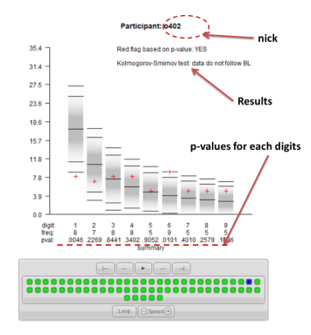
The final stage is discussing the results of the classroom experiment. After introducing BL in a functional form with relevant real-life examples, the teacher should present its applications in detecting tax fraud (Nigrini, 2012; Simkin, 2010) and show the summary visualization of the results of the antifraud procedures applied to the experimental data. The analysis was performed using the R-CRAN package BenfordTests (Joenssen, 2015). The first stage of the procedure is a "red flag indicator" based on the digits' p-value. If there is a statistically significant difference between the frequency assigned by the participant and the frequency predicted by BL (i.e., if the p-value is higher than 0.1), the flag is set. The second stage is the Kolmogorov-Smirnov goodness-of-fit test. With the use of the automatizing R codes, the visualization is ready immediately after finishing the experiment (see supplementary online materials).

Source: authors' own work, based on R and BenfordTests (Joenssen, 2015), available in online materials.
An essential part of the visualization is to present the participants' nicknames only on the screen. The results are presented publicly, and the students can easily see and recognize their responses while remaining completely anonymous. In psychology, the experience can be personally transformative if it changes one's point of view (Paul, 2013). Being caught cheating in this way is a valid form of experience, even if it is only a game. If future decisions on whether to cheat is based on a perception of the probability of not being caught, then the obtained results leave no illusions. Even simple statistical procedures can indicate fraud exceptionally effectively. The experiment was conducted twice (with groups of 10 and 60 people), and all the students were flagged.
The simplicity of the BL test (see Fig. 6) can be good motivation for students to conduct their own investigation. The students can apply the ready-to-use R codes, enabling them to apply the BL test with no prior experience in coding. The rest of the attached codes are more complicated, mainly because of the publication purposes, but even students and teachers with little or no coding experience can use and modify them; the codes are free and available for everyone.
There are numerous sets of economic data that have not been tested for the possibility of mistakes, errors, tax fraud or even the scientific fraud. In international trade, importers usually avoid reporting large volumes, as this may require a higher tariff rate. From this perspective, international trade statistics can be an exciting test area for applying BL in order to identify fraud.
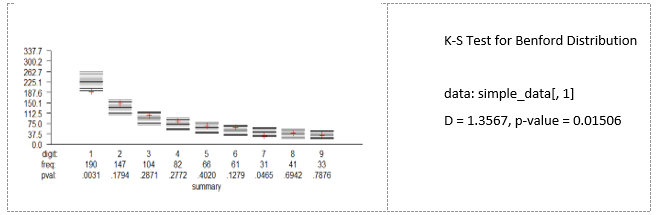

Source: authors' own work based on IMF Direction of Trade statistics and R package BenfordTests (Joenssen, 2015), available in online materials.
The empirical distributions of the first digits are not consistent with BL distributions for some years (see Fig. 7 and supplementary online materials). For such a large sample, the presented deviation from BL can be a good motivation for further detailed investigation.
For students of more advanced quantitative methods, it is worth discussing two papers devoted to i) one of the most straightforward explanations of BL (Fewster, 2009); and ii) why the presented explanations of BL are still not satisfactory (Berger & Hill, 2011). The latter paper criticizes "folk" explanations of BL (such as the "birthday paradox"), pointing out that although they seem to be intuitive, they do not pass the test of solid mathematical analysis. In other words, BL still remains a kind of mystery.
Playing with BL accidentally creates mystery and the atmosphere of crime puzzles. For a group of MA students, this issue was so interesting that they spontaneously came up with the idea of a contest. During the contest, a team of "creative accountants" and another of the "tax authority" competed. The goal of the former team was to generate such datasets that would not be detectable by the latter group. After some modifications, the contest seems to have become an auspicious tool to inspire students to make additional effort during quantitative methods courses.
The mystery of BL touched the authors too. How can one explain the result of a simple MC experiment? The experiment can be conducted in N-steps.
Step 1: From the sample of natural numbers ranked from 1 to 999, a number p1 is randomly picked using a random number generator with a uniform distribution.
Step 2: From the sample of natural numbers ranked from 1 to p1, a number p2 is drawn using the same techniques as in the first step.
Step 3: From the sample of natural numbers ranked from 1 to p2, a number p3 is drawn using the same technique as in step one. [...]
Step N: From the sample of natural numbers ranked from 1 to pn, a number p(n+1) is drawn using the same technique as in step one.
The entire procedure should be replicated 10,000 times, which should result in N vectors containing all the randomly picked numbers p for each step. For each such vector, the first-digit law is tested. The results obtained from step 1 are similar to the ball drawing simulation with a uniform distribution. More steps causes number 1 to be more frequent (see Fig. 8), and the distribution approaches the BL pattern. This creates a puzzle: why are only 3 steps required to generate the numbers which follow BL? For more than 3 steps, the simulated distribution moves away from the theoretical distribution: digit 1 becomes much more frequent.


Source: authors' own application, based on R and BenfordTests (Joenssen, 2015), available in online materials.
The experiment and the prepared MC simulations can be used in a wide range of academic courses, such as accounting, applied microeconomics, and quantitative methods. The actual scheme chosen to present the material depends on the subject of study. The presented scheme was designed around an Applied Microeconomic course for data science students, but the materials can be used like Lego bricks and easily adjusted to one's needs.
Conclusions
This paper presents a simple in-class experiment and Monte Carlo simulations. Its goals are twofold. The first is to familiarize the students with the existence and the properties BL, which is one of the "gems of statistical folklore" (Berger & Hill, 2011). The second is to achieve vital teaching goals. One of the leading teaching goals in this experiment was to train the students' skills in the realistic perception of probabilities, which does not currently form part of microeconomics courses. The experiment, therefore, attempts to demonstrate that the simplified perception of probabilities may result in a failure during real-life data analyses. The additional goal was to train the students' skills in the critical assessment of data, as the frequent use of unreliable or fake data is a continuing problem in the social sciences. The demonstration of how easily fraud may be detected is expected to diminish the motivation of students to cheat in their courses, or, even in their professional career. Finally, the presented classroom experiment can be used to familiarize the students with the basic IT tools, necessary for the simple data analysis.
The authors will continue to create new materials concerning BL and generally probability and risk perception. We are happy to share new experiments and simulations at our site.
References
- Benford, F. (1938). The Law of Anomalous Numbers. Proceedings of the American Philosophical Society, 78(4), 551-572. http://www.jstor.org/stable/984802
- Berger, A., & Hill, T. P. (2011). Benford's law strikes back: no simple explanation in sight for mathematical gem. The Mathematical Intelligencer, 33(1), 85-91.
- Berger, A., & Hill, T. P. (2015). An introduction to Benford's law. Princeton, NJ: Princeton University Press.
- Carslaw, C. A. P. N. (1988). Anomalies in Income Numbers: Evidence of Goal Oriented Behavior. The Accounting Review, 63(2), 321-327. http://www.jstor.org/stable/info/248109
- Cho, W. K. T., & Gaines, B. J. (2007). Breaking the (Benford's) law: Statistical fraud detection in campaign finance. American Statistician, 61(3), 218-223. DOI: https://doi.org/10.1198/000313007X223496
- Drake, P. D., & Nigrini, M. J. (2000). Computer assisted analytical procedures using Benford's Law. Journal of Accounting Education, 18(2), 127-146. DOI: https://doi.org/10.1016/S0748-5751(00)00008-7
- Durtschi, C., Hillison, W., & Pacini, C. (2004). The Effective Use of Benford's 'Benford's s Law to Assist in Detecting Fraud in Accounting Data. Journal of Forensic Accounting, 5(1), 17-34.
- Ettredge, M. L., & Srivastava, R. P. (1999). Using Digital Analysis to Enhance Data Integrity. Issues in Accounting Education, 14(4), 675-690. DOI: https://doi.org/10.2308/iace.1999.14.4.675
- Falk, R., & Konold, C. (1997). Making sense of randomness: implicit encoding as a basis for judgment. Psychological Review, 104(2), 301-318. DOI: 10.1037/0033-295X.104.2.301
- Fewster, R. M. (2009). A simple explanation of Benford's law. American Statistician, 63(1), 26-32. DOI: https://doi.org/10.1198/tast.2009.0005
- Frank, R., & Cartwright, E. (2013). Microeconomics and behaviour. McGraw Hill.
- Furlan, L. (1948). Das Harmoniegesetz der Statistik: Eine Untersuchungüber die metrische Interdependenz der sozialen Erscheinungen. Basel, Schwitzerland: Verlag für Recht und Gesellschaft.
- Gabaix, X. (2016). Power Laws in Economics: An Introduction. Journal of Economic Perspectives, 30(1), 185-206. DOI: https://doi.org/10.1257/jep.30.1.185
- Gartner. (2015). APM - Gartner IT Glossary. Retrieved from http://www.gartner.com/it-glossary/application-performance-monitoring-apm/
- Gauvrit, N., Houillon, J. C., & Delahaye, J. P. (2017). Generalized Benford's law as a lie detector. Advances in Cognitive Psychology, 13(2), 121-127. DOI: https://doi.org/10.5709/acp-0212-x
- Geyer, D. (2010). Detecting Fraud in Financial Data Sets. Journal of Business & Economics Research, 8(7), 75-83.
- Gigerenzer, G. (2015). Calculated risks: How to know when numbers deceive you. New York: Simon and Schuster.
- Giles, D. E. (2007). Benford's law and naturally occurring prices in certain ebaY auctions. Applied Economics Letters, 14(3), 157-161. DOI: https://doi.org/10.1080/13504850500425667
- Henselmann, K., Scherr, E., & Ditter, D. (2012). Applying Benford's Law to individual financial reports: An empirical investigation on the basis of SEC XBRL filings. Working papers in accounting valuation auditing. Retrieved from https://ideas.repec.org/p/zbw/fauacc/20121r.html
- Hill, T. (1995). A statistical derivation of the significant-digit law. Statistical Science, 10(4), 354-363. DOI: 10.1214/ss/1177009869
- Ioannidis, J., & Doucouliagos, C. (2013). What's to know about the credibility of empirical economics? Journal of Economic Surveys, 27(5), 997-1004. DOI: https://doi.org/10.1111/joes.12032
- Janvrin, D. J., & Weidenmier Watson, M. (2017). "Big Data": A new twist to accounting. Journal of Accounting Education, 38, 3-8. DOI: https://doi.org/10.1016/j.jaccedu.2016.12.009
- Joenssen, D. W. (2015). Benford's Tests: statistical tests for evaluating conformity to Benford's law. Computer Software. https://cran.r-project.org/web/packages/BenfordTests/index.html
- Joyner, E. (2011). Detecting and preventing fraud in financial institutions. SAS Global Forum 2011, 1-16. Retrieved from http://support.sas.com/resources/papers/proceedings11/029-2011.pdf
- Kiuila, O. (2018). Decarbonisation perspectives for the Polish economy. Energy Policy, 118, 69-76. DOI: https://doi.org/10.1016/j.enpol.2018.03.048
- Ley, E. (1996). On the Peculiar Distribution of the U.S. Stock Indexes' Digits. American Statistician, 50(4), 311-313. DOI: https://doi.org/10.1080/00031305.1996.10473558
- McConnell, C. R., Brue, S. L., Flynn, S. M., (2014). Microeconomics. McGraw-Hill Education; 20th edition.
- Michalski, T., & Stoltz, G. (2013). Do countries falsify economic data strategically? Some evidence that they might. Review of Economics and Statistics, 95(2), 591-616. https://doi.org/10.1162/REST_a_00274
- Newcomb, S. (1881). Note on the frequency of use of the different digits in natural numbers. American Journal of Mathematics, 4(1), 39-40.
- Nigrini, M. (1999). I've Got Your Number: How a mathematical phenomenon can help CPAs uncover fraud and other irregularities. Journal of Accountancy, 187(5), 79-83. Retrieved from http://www.journalofaccountancy.com/Issues/1999/May/nigrini
- Nigrini, M. J. (1996). A Taxpayer Compliance Application of Benford's Law. Journal of the American Taxation Association, 18(1), 72-91. Retrieved from https://www.econbiz.de/Record/a-taxpayer-compliance-application-of-benford-s-law-nigrini-mark-john/10001202885
- Nigrini, M. J. (2012). Forensic Analytics: Methods and Techniques for Forensic Accounting Investigations. DOI: https://doi.org/10.1002/9781118386798
- Noether, G. E. (1963). Note on the Kolmogorov statistic in the discrete case. Metrika: International Journal for Theoretical and Applied Statistics, 7(1), 115-116. DOI: https://doi.org/10.1007/BF02613966
- Norton, M. I., & Ariely, D. (2011). Building a better America-one wealth quintile at a time. Perspectives on Psychological Science, 6(1), 9-12. DOI: https://doi.org/10.1177/1745691610393524
- Paul, L. A. (2013). Teaching Guide for Transformative Experience. Retrieved from https://lapaul.org/papers/teaching-guide-for-transformative-experience.pdf
- Sambridge, M., & Tkalčic, H. (2010). Benford's law in the natural sciences. Geophysical Research Letters, 37(22). DOI: https://doi.org/10.1029/2010GL044830
- Sambridge, M., Tkalčić, H. & Arroucau, P. (2011). Benford's Law of First Digits: From Mathematical Curiosity to Change Detector. Asia Pacific Mathematics Newsletter, 1(4), 1-5.
- Simkin, M. G. (2010). Using Spreadsheets and Benford's Law to Test Accounting Data. ISACA Journal, 1, 47-52.
- Stephens, M. A. (1970). Use of the Kolmogorov-Smirnov, Cramer-Von Mises and Related Statistics Without Extensive Tables. Journal of the Royal Statistical Society. Series B (Methodological), 32(1), 115-122. DOI: https://doi.org/10.1111/j.2517-6161.1970.tb00821.x
- Varian, H. R. (1972) Benford's Law. The American Statistician, 26, 65-66.
- Varian, H. R. (2014). Intermediate Microeconomics: A Modern Approach: Ninth International Student Edition. New York: WW Norton & Company.
- Watt, R. (2011). The Microeconomics of Risk and Information. New York: Palgrave Macmillan.
- Xie, Y. (2013). Animation: An R Package for Creating Animations and Demonstrating Statistical Methods. Journal of Statistical Software, 53(1). DOI: https://doi.org/10.18637/jss.v053.i01
- Yang, S., & Wei, L. (2010). Detecting money laundering using filtering techniques: A multiple-criteria index. Journal of Economic Policy Reform, 13(2), 159-178. DOI: https://doi.org/10.1080/17487871003700796
- Zipf, G. (1936). The Psychobiology of Language. London: Routledge.



